Spherical Embeddings or Spherical Fourier Neural Operators
22.01.2025Although our planet is a sphere and therefor all weather and climate processes operate on sphere, Deep Learning Weather Models very commonly operate on different rectangular projections of the sphere. This introduces increasingly larger errors the closer a location is to the poles. Among works, that explore spherical structures for modelling, are those that use spherical harmonics.
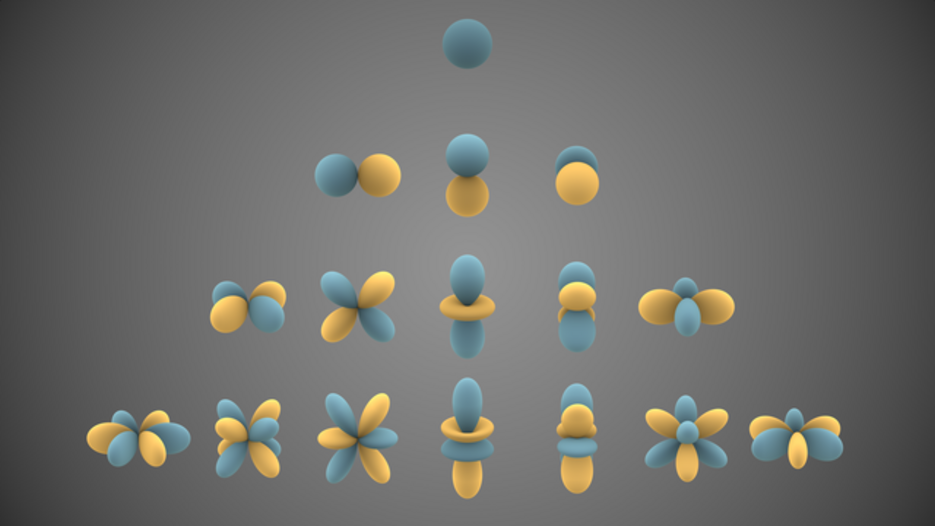
This tasks focuses on two approaches that rely on spherical harmonics: Spherical Fourier Embeddings [1] and Spherical Fourier Neural Operators [2].
Spherical Fourier Embeddings (SFE) calculate embeddings of the data using the Spherical Fourier Transform. Then models are trained on the embedded data. Spherical Fourier Neural Operators (SFNO) learn operators using Spherical Fourier Transforms inside network blocks similar to ResNet blocks. These blocks can be used to create ResNets and are trained on spherical data.
You will train SFE and SFNO models on spherical datasets and evaluate model performances with respect to standard quality metrics. Additionally, you will investigate the training process with regards to ressource consumption and training and preprocessing times.
Your profile:
• student of computer science, maths, physics, natural sciences
• experience in programming python
• ideally experience with git
• ideally experience with PyTorch or similar deep learning frameworks
Supervisor: Anna Krause
[1] Marc Rußwurm et al., Geographic Location Encoding with Spherical Harmonics and Sinusoidal Representation Networks, 2024, https://arxiv.org/abs/2310.06743.
[2] Boris Bonev et al., Spherical Fourier Neural Operators: Learning Stable Dynamics on the Sphere, 2023, https://arxiv.org/abs/2306.03838